Contents
Solving Asymptotics-based Evolution Equations !
Evolution Equation Modeling
For propagating fronts, considered as density surface discontinuities, a class of EEM (Evolution Equation Modeling) can be derived by analytically solving the set of
- Euler equations
- Rankine-Hugoniot jump relationships
- a local kinematic relation defining the local front velocity (possibly depending on local curvature).
when the density contrast between 'hot' and 'cold' fluids is asymptotically small.
This Sivashinsky-type perturbative approach leads to non-linear non-local EE, with easily identified meaningful terms.
FLAMEX is a suite of solvers able to compute high accuracy solutions to asymptotic expansion based evolution equations (EE), of 1rt or 2nd order in time.
Main features
- Solving first-order or second order EE in the Fourier or Fourier-Legendre basis.
- Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005)
- EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients, tangential velocity, gravity effects...
- Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence')

|
Sample Results
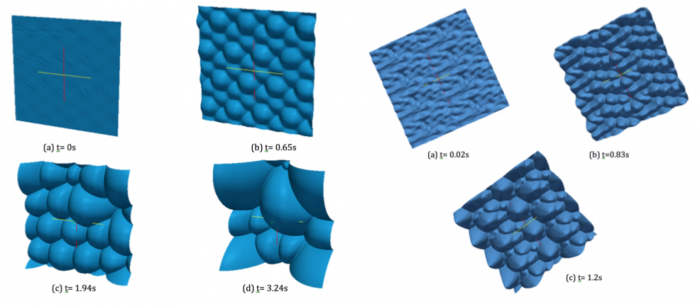
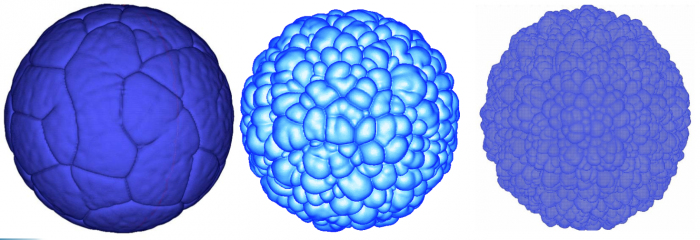
We show below a short gallery of pictures obtained using the FLAMEX solver.
|
|
Notice the 'soccer-ball' and 'cauliflower' aspects of the front, as described by Zel'dovitch in the 40's.
- See also some quantitative comparisons between FLAMEX and DNS (HALLEGRO) results at [1]
- More details (and comparisons with experimental results) in [2], [3]
Modules for asymptotic modeling of Flame-Balls
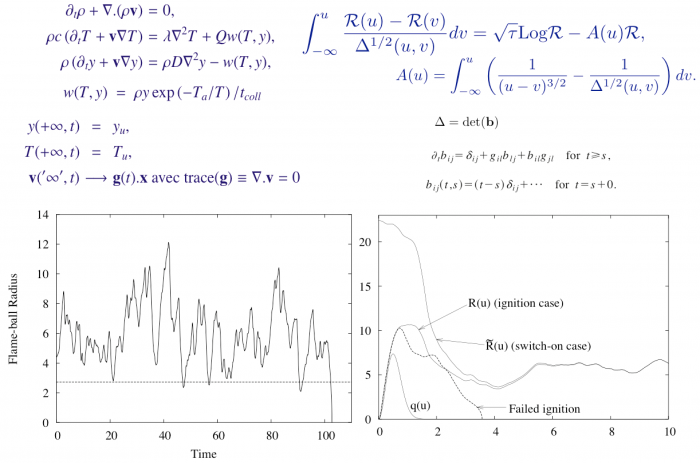
Some modules of FLAMEX have been devoted to the numerical solution to flame-balls (FB) dynamics. Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic) integrodifferential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor \(g(t)\). For a diagonal \(g(t)\) deduced from random Markov processes of the Ornstein-Uhlenbeck type, or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that
- flame balls can definitely live for much longer than their time of spontaneous expansion/collapse;
- large enough values of lifetimes are compatible with Poisson statistics;
- the variations of the lifetime with the characteristics of \(g(t)\) mirror the latter’s statistics, more precisely that of trace(\(g^2\)).
|
Participants
Yves D'Angelo, Guy Joulin, Eric Albin, Rui Rego, Gaël Boury, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji.
