DyCo also stands for Dynamiques Couplées ! (in French).
The DYCO Solvers suite
DYCO is a suite of solvers able to compute high accuracy solutions to non-linear stock/flow potentials coupled equations. It is based on a nodal approach strategy.
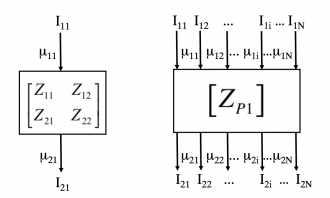
|
|
|
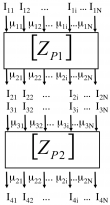
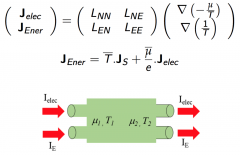
Left: Elementary Cell, Coupled potentials (1 or N coupled potentials, also in series)
Right: example in the thermo-electric context
Main features
- Nodal description of the considered network.
- Non linear Onsager type coupling between forces & fluxes.
- Steady, pseudo-unsteady & unsteady computations.
- Handle local to global scales (i.e. from coarse-grain to fine tuning).
- Possibly complex non-homogeneous structures and topologies.
- Possibly anisotropic, discontinuous coupling coefficients; potentials & time dependency can also be included.
- Local flux continuity enforced
- Allows for lighter/heavier computations and technological “optimization” !
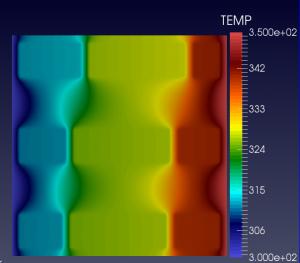
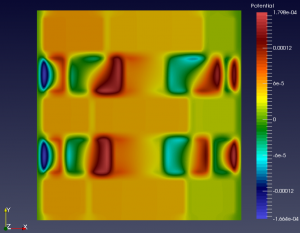
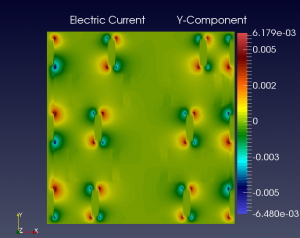
Sample Results
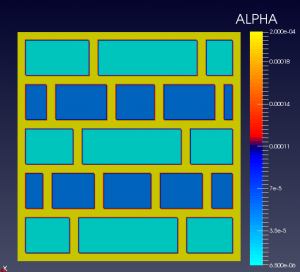
We show below a short gallery of pictures obtained using the DYCO solver, in the thermo-electric context.
|
|
|
|

|

|
In both cases, BC are Homogeneous Neumann and/or Non-Homogeneous Dirichlet.
Each elementary cell is of the non-ideal (non-linear) type.
Sub-modules
More specific sub-modules of DYCO shall be devoted to the numerical solution of coupled stock/flow potentials dynamics in the ecological economics and biological contexts.
Participants
Yves D'Angelo, Christophe Goupil, Eric Herbert, Xanthippi Zianni
