(→The FLAMEX Solver) |
|||
| (28 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[File:Flamex.jpg|right|240px|Yves D'Angelo]] | |
| − | [[File:Flamex.jpg|240px]] | + | __TOC__ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Solving Asymptotics-based Evolution Equations and networks ! | |
| − | == Main features== | + | ==Evolution Equation Modeling for wrinkled fronts== |
| − | * Solving first-order or second order EE in the Fourier or Fourier-Legendre basis. | + | *For propagating fronts, considered as density surface discontinuities, a class of EEM (Evolution Equation Modeling) can be derived by analytically solving the set of |
| − | * Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005) | + | ** Euler equations |
| + | ** Rankine-Hugoniot jump relationships | ||
| + | ** a local kinematic relation defining the local front velocity (possibly depending on local curvature). | ||
| + | when the density contrast <math> \alpha </math> between 'hot' and 'cold' fluids is asymptotically small. | ||
| + | |||
| + | * This Sivashinsky-type perturbative approach leads to non-linear non-local Evolution Equations. At first (and second) order in <math> \alpha </math>, and 1st order in time, each building-block term in the EE corresponds to a clearly identified phenomenon, like Landau-Darrieus hydrodynamic instability, Huygens-type propagation and curvature thermo-diffusive contribution. | ||
| + | |||
| + | * FLAMEX is made of a suite of solvers, able to compute | ||
| + | ** EEM: high accuracy solutions to asymptotic expansion based evolution equations, of 1rt or 2nd order in time for wrinkled propagating fronts; | ||
| + | ** FB: integro-differential stochastic evolution equations for flame-balls; | ||
| + | ** PF: modeling and resolution of percolating fronts in disordered pre-mixtures. | ||
| + | |||
| + | ==Main features of the EEM Module== | ||
| + | * Solving first-order or second-order in time EE in the Fourier or Fourier-Legendre basis. | ||
| + | * Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005). | ||
* EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients, tangential velocity, gravity effects... | * EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients, tangential velocity, gravity effects... | ||
| − | * Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence') | + | * Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence'). |
{| class="wikitable" | {| class="wikitable" | ||
|+ Examples of first-order in time obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts | |+ Examples of first-order in time obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts | ||
| − | |[[File:OUIEEM-1D-2D.png| | + | |[[File:OUIEEM-1D-2D.png|350 px]] |
| − | |[[File:OUIEqEEM_1D.png| | + | |[[File:OUIEqEEM_1D.png|350 px]] |
|} | |} | ||
| − | == Sample Results == | + | == Sample Results of the EEM module== |
| − | We show below a short gallery of pictures obtained using the FLAMEX solver. | + | We show below a short gallery of pictures obtained using the EEM module of the FLAMEX solver. |
{| class="wikitable" | {| class="wikitable" | ||
|+ Sample results for 3D planar fronts | |+ Sample results for 3D planar fronts | ||
| Line 37: | Line 45: | ||
* More details (and comparisons with experimental results) in [http://dx.doi.org/10.1016/j.ijnonlinmec.2011.05.018], [http://dx.doi.org/10.1016/j.combustflame.2011.12.019] | * More details (and comparisons with experimental results) in [http://dx.doi.org/10.1016/j.ijnonlinmec.2011.05.018], [http://dx.doi.org/10.1016/j.combustflame.2011.12.019] | ||
| − | == | + | |
| − | + | ==Module for asymptotic modeling of Flame-Balls, FB== | |
| − | Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic) | + | |
| − | For a diagonal g(t) deduced from random Markov processes of the Ornstein-Uhlenbeck type, | + | Some modules of FLAMEX have been devoted to the numerical solution to flame-balls (FB) dynamics. |
| + | Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic) integro-differential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor <math>g(t)</math>. | ||
| + | For a diagonal <math>g(t)</math> deduced from random Markov processes of the Ornstein-Uhlenbeck type, | ||
or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that | or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that | ||
* flame balls can definitely live for much longer than their time of spontaneous expansion/collapse; | * flame balls can definitely live for much longer than their time of spontaneous expansion/collapse; | ||
* large enough values of lifetimes are compatible with Poisson statistics; | * large enough values of lifetimes are compatible with Poisson statistics; | ||
| − | * the variations of the lifetime with the characteristics of g(t) mirror the latter’s statistics, more precisely that of trace(g | + | * the variations of the lifetime with the characteristics of <math>g(t)</math> mirror the latter’s statistics, more precisely that of trace(<math>g^2</math>). |
| − | + | ||
| − | | | + | <center>[[File:Fbdynamics.png|500 px]]</center> |
| − | + | <center>System of equations, integro-differential evolution equation and sample results of FB radius dynamics</center> | |
| + | |||
| + | |||
| + | ==Module for percolating fronts PF== | ||
| + | In solid-like pre-mixtures, when the initial reactant content and/or reactivity are maxima along the axis of straight channels, curved flames are able to propagate under conditions. Such individual channels (and the conditions for propagation) can be lumped as building blocks of a larger percolation network. | ||
| + | |||
| + | Possible applications deal with wildfires propagation, sprays, inhomogeneous reacting media. | ||
| + | |||
| + | <center>[[File:Oe.png|350 px]]</center> | ||
| + | <center>Propagative fronts in non-diffusing disordered premixtures: single-channel flame and large scale network modeling.</center> | ||
| + | |||
| + | {| class="wikitable" style="margin: 1em auto 1em auto;" | ||
| + | |{{#widget:YouTube|id=kSwhon6gQis |width=300 |height=250}} | ||
| + | |{{#widget:YouTube|id=YxCRj6N7qY8 |width=400 |height=250}} | ||
|} | |} | ||
| + | LEFT : FD DNS of a single-channel flame, showing pulsating instabilities (iso-temperature). A layer of heated unburnt material is formed then very quickly ‘shaved’ by a secondary channel-flame. This may even take place on top of the secondary flames themselves. | ||
| + | |||
| + | RIGHT : Numerical Simulation of the large-scale propagation (percolation) of a reacting front in non-diffusing disordered pre-mixtures (as a network collection of single-channel flames). The density of passing links fraction is increased from <math>p=0.51</math> to <math>p=0.8</math>. | ||
| + | |||
| + | <!--foo More details in [http://dx.doi.org/10.1080/13647830802043978].--> | ||
== Participants == | == Participants == | ||
| − | + | Guy Joulin, Rui Rego, Olivier Esnault, Gaël Boury, Eric Albin, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji, Yves D'Angelo. | |
Latest revision as of 19:01, 23 July 2023
Contents
Solving Asymptotics-based Evolution Equations and networks !
Evolution Equation Modeling for wrinkled fronts
- For propagating fronts, considered as density surface discontinuities, a class of EEM (Evolution Equation Modeling) can be derived by analytically solving the set of
- Euler equations
- Rankine-Hugoniot jump relationships
- a local kinematic relation defining the local front velocity (possibly depending on local curvature).
when the density contrast \( \alpha \) between 'hot' and 'cold' fluids is asymptotically small.
- This Sivashinsky-type perturbative approach leads to non-linear non-local Evolution Equations. At first (and second) order in \( \alpha \), and 1st order in time, each building-block term in the EE corresponds to a clearly identified phenomenon, like Landau-Darrieus hydrodynamic instability, Huygens-type propagation and curvature thermo-diffusive contribution.
- FLAMEX is made of a suite of solvers, able to compute
- EEM: high accuracy solutions to asymptotic expansion based evolution equations, of 1rt or 2nd order in time for wrinkled propagating fronts;
- FB: integro-differential stochastic evolution equations for flame-balls;
- PF: modeling and resolution of percolating fronts in disordered pre-mixtures.
Main features of the EEM Module
- Solving first-order or second-order in time EE in the Fourier or Fourier-Legendre basis.
- Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005).
- EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients, tangential velocity, gravity effects...
- Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence').

|
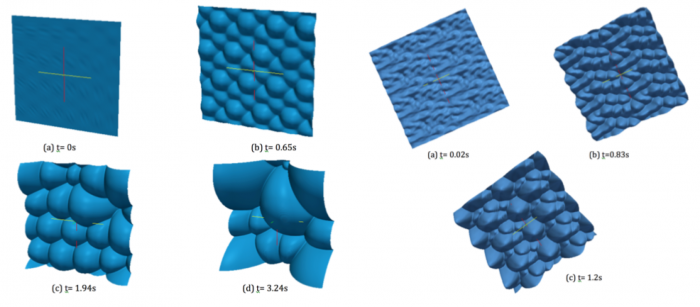
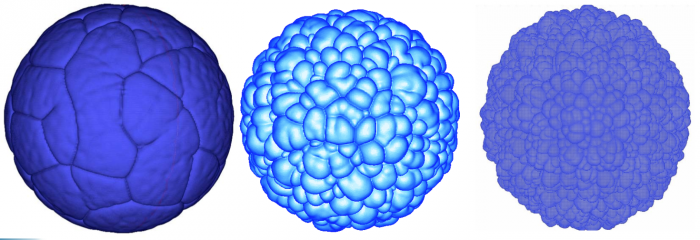
Sample Results of the EEM module
We show below a short gallery of pictures obtained using the EEM module of the FLAMEX solver.
|
|
Notice the 'soccer-ball' and 'cauliflower' aspects of the front, as described by Zel'dovitch in the 40's.
- See also some quantitative comparisons between FLAMEX and DNS (HALLEGRO) results at [1]
- More details (and comparisons with experimental results) in [2], [3]
Module for asymptotic modeling of Flame-Balls, FB
Some modules of FLAMEX have been devoted to the numerical solution to flame-balls (FB) dynamics. Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic) integro-differential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor \(g(t)\). For a diagonal \(g(t)\) deduced from random Markov processes of the Ornstein-Uhlenbeck type, or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that
- flame balls can definitely live for much longer than their time of spontaneous expansion/collapse;
- large enough values of lifetimes are compatible with Poisson statistics;
- the variations of the lifetime with the characteristics of \(g(t)\) mirror the latter’s statistics, more precisely that of trace(\(g^2\)).
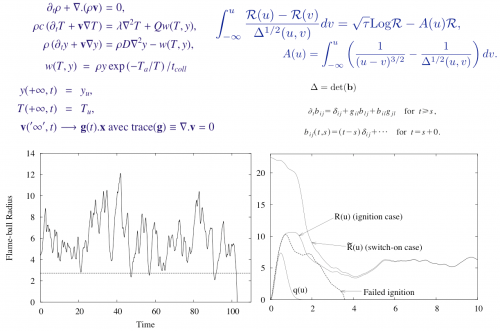
Module for percolating fronts PF
In solid-like pre-mixtures, when the initial reactant content and/or reactivity are maxima along the axis of straight channels, curved flames are able to propagate under conditions. Such individual channels (and the conditions for propagation) can be lumped as building blocks of a larger percolation network.
Possible applications deal with wildfires propagation, sprays, inhomogeneous reacting media.
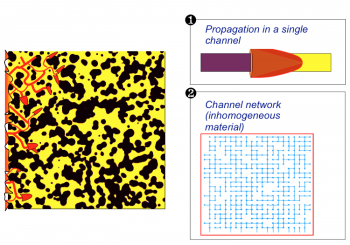
LEFT : FD DNS of a single-channel flame, showing pulsating instabilities (iso-temperature). A layer of heated unburnt material is formed then very quickly ‘shaved’ by a secondary channel-flame. This may even take place on top of the secondary flames themselves.
RIGHT : Numerical Simulation of the large-scale propagation (percolation) of a reacting front in non-diffusing disordered pre-mixtures (as a network collection of single-channel flames). The density of passing links fraction is increased from \(p=0.51\) to \(p=0.8\).
Participants
Guy Joulin, Rui Rego, Olivier Esnault, Gaël Boury, Eric Albin, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji, Yves D'Angelo.
