dyco

The FLAMEX Solver

For propagating fronts, considered as density surface discontinuities, EEM (Evolution Equation Modeling) can be derived by analytically solving the set of

• Euler equations
• Rankine-Hugoniot jump relationships
• a local kinematic relation defining the local front velocity (e.g. with respect to local curvature).

when the density contrast between 'hot' and 'cold' fluids is asymptotically small.

This Sivashinsky-type perturbative approach leads to non-linear non-local EE, with easily identified meaningful terms.

FLAMEX is a suite of solvers able to compute high accuracy solutions to asymptotic expansion based evolution equations (EE), of 1rt or 2nd order in time.

Main features

• Solving first-order or second order EE in the Fourier or Fourier-Legendre basis.
• Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005)
• EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients, tangential velocity, gravity effects...
• Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence')

Examples of first-order in time obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts

Sample Results

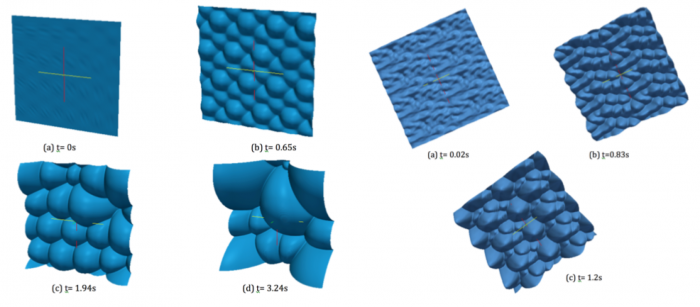
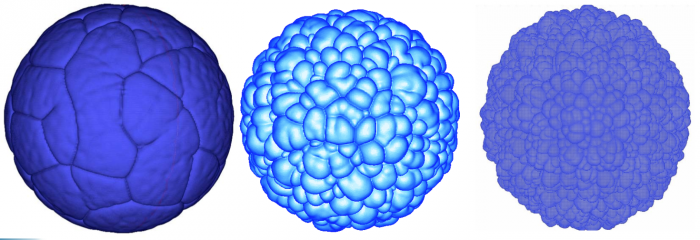
We show below a short gallery of pictures obtained using the FLAMEX solver.

Sample results for 3D planar fronts

Sample results for 3D expanding fronts with variable turbulence intensity,

Notice the 'soccer-ball' and 'cauliflower' aspects of the front, as described by Zel'dovitch in the 40's.

• See also some quantitative comparisons between FLAMEX and DNS (HALLEGRO) results at [1]
• More details (and comparisons with experimental results) in [2], [3]

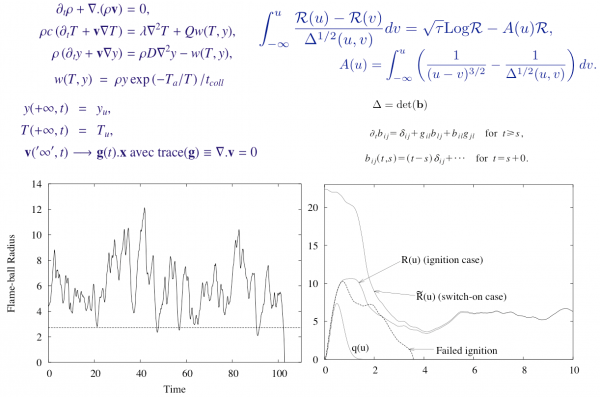
Sub-module for asymptotic modeling of Flame-Balls

A sub-module of FLAMEX has been devoted to the numerical solution to flame-balls (FB) dynamics. Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic) integrodifferential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor g(t). For a diagonal g(t) deduced from random Markov processes of the Ornstein-Uhlenbeck type, or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that

• flame balls can definitely live for much longer than their time of spontaneous expansion/collapse;
• large enough values of lifetimes are compatible with Poisson statistics;
• the variations of the lifetime with the characteristics of g(t) mirror the latter’s statistics, more precisely that of trace(g*g).

System of equations, EEM and sample results of FB radius dynamics

Participants

Yves D'Angelo, Guy Joulin, Eric Albin, Rui Rego, Gaël Boury, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji.