dyco

The FLAMEX Solver

FLAMEX is a suite of solvers able to compute high accuracy solutions to asymptotics-based evolution equations (EE). For propagatong fronts, the EEM (Evolution Equation Modeling) can be found by solving exactly the set of

• Euler equations
• Rankine-Hugoniot jump relations
• the local kinematic relation defining the local front velocity (e.g. with respect to local curvature).

when the density contrast between 'hot' and 'cold' fluids is asymptotically small.

Examples of obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts

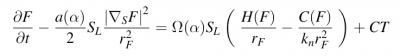
Main features

• Solving first-order or second order EE in the Fourier or Fourier-Legendre basis.
• Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005)
• Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence')

Sub-module for asymptotic modeling of Flame-Balls

A sub-module of FLAMEX has also been devoted to the

Sample Results

• See some comparisons between FLAMEX and DNS (HALLEGRO) results [1]
• More details (and comparisons with experimental results) in