| (6 intermediate revisions by 2 users not shown) | |||
| Line 96: | Line 96: | ||
* from a mathematical point of view, using statistical tools as well as probabilistic and SDE and PDE tools, we wish to build and assess robust and versatile models, analyze their mathematical properties as well as design (and also possibly analyze) adapted efficient numerical methods. We aim at both formal and (possibly) rigorous derivations of the models. | * from a mathematical point of view, using statistical tools as well as probabilistic and SDE and PDE tools, we wish to build and assess robust and versatile models, analyze their mathematical properties as well as design (and also possibly analyze) adapted efficient numerical methods. We aim at both formal and (possibly) rigorous derivations of the models. | ||
| − | === Participants === | + | === <strong>Participants </strong>=== |
| − | Yves D'Angelo (Scientific Coordinator | + | <br/> |
| − | Rémi Catellier, Laurent Monasse (LJAD) | + | Yves D'Angelo (Scientific Coordinator), Rémi Catellier, Laurent Monasse, Claire Guerrier , Thierry Goudon (LJAD Nice) |
| − | Florence Chapeland-Leclerc, Gwenaël Ruprich-Robert, (B2C Group, LIED) <br/ > | + | <br/> |
| − | Eric Herbert, Cécilia Bobée, Pascal David ( | + | Florence Chapeland-Leclerc, Gwenaël Ruprich-Robert, Eva Cabet (B2C Group, LIED) |
| − | <br/ > | + | <br/> |
| − | <br/ > | + | Eric Herbert, Cécilia Bobée, Pascal David, Christophe Lalanne, (Physics Group, LIED) |
| − | <br/ > Franco Flandoli (Scuola Normale di Pisa). | + | <br/> Amandine Véber (MAP5, Paris), |
| + | <br/> Milica Tomasevic (CMAP, Ecole Polytechnique) | ||
| + | <br/> | ||
| + | <br/> <strong>Former participants</strong> | ||
| + | <br/> Adélaïde Olivier (Math Lab at Orsay), | ||
| + | <br/> Franco Flandoli (Scuola Normale di Pisa). | ||
| + | <br/> | ||
| + | <br/> <strong>PhD Students and Interns</strong> | ||
| + | <br/> Clara Ledoux | ||
| + | <br/> Moira Lampe | ||
| + | <br/> Nicolas Fricker | ||
| + | <br/> Sebastian Baudelet | ||
| + | <br/> Thibault Chassereau | ||
| + | <br/> Lena Kuwata | ||
| + | <br/> Aurélien Corrado | ||
Latest revision as of 13:41, 29 March 2023
Contents
Dynamics of Random
Expanding networks Analysis,
modeling and simulation of Multi-Scale spatial exploration, spreading and morphogenesis under constraints.
Studying the constrained hyphal growth in the filamentous fungus Podospora anserina
Context
How fungi or plants invade a medium, how sexually transmitted diseases spread over a population, how cancer tumors grow in human bodies, how communication routes densify, are questions that may seem to refer to quite unrelated problems. However, the structure, dynamics and shape of the underlying network may rely on very similar models.
The nature of such networks is not uniquely defined: some examples are informational networks (of relation between individuals, citation graphs,...), technological (power grids, public transportation, computer network,...), or biological (vascular, biochemical, neural network,...). In all the aforementioned examples, transformation arises from individuals, be it the development of a new connection between existing entities, as it often appears in neurons, or the introduction of a new individual in the system. All these contributions sum up to the evolution of the network as a unit on the macroscopic level.
Modeling of such intricate processes ranges from simple explanatory toy-models to more realistic approaches, which need to be able to capture modifications at different scales. This can be achieved by linking microscopic objects, which describe individuals, with their collective mean behavior. Techniques borrowing from statistical physics for the analysis of nonlinear, non-equilibrium physical systems in the study of such collective behavior are of increasing use, in e.g. social, economical or biological systems.
The expansion of such networks may also be hindered by internal or external constraints which can significantly affect the observed results and patterns. When explicitly including the spatial dimension, the models considered may provide a pertinent description of the interaction processes at the small (micro) scale as well as the large (macro)scale featuring the emerging behavior, possibly under the form of a (thin) propagating front. The modeling and analysis of such dynamical processes within a multi-scale framework, where the different granularities of the system are to be considered, is a complex research field, that requires involving various disciplines.
In the DREAMS project, we want to specifically address the modeling and analysis of the expanding interconnected hyphal network (the vegetative filaments produced to form the mycelium) of the fungus Podospora anserina.

|

|
|
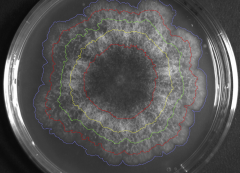
Left: Example of the reconstitution (as reconstructed by numerous pictures juxtaposition and conformal mapping, 112 tiles) of the complete thallus of P. anserina, grown 23h on a Petri dish. The diameter is approx. 20 mm.
Center: small-scale (approx. 1 mm) image processing and vectorization; raw data from experiment (at time t=18h) is superimposed to the output of the vectorization process.
Right: observed macroscopic mycelium (diameter around 8 cm) after a 4 day-growth. Note the expanding front, represented by the hyphal concentration isovalues shown at different times (colored
lines).
A toy-model: Podospora Anserina
In real-life conditions, P. anserina is a coprophilous filamentous ascomycete that grows on herbivore dungs, a highly competitive habitat where several dozens of species are present and feed on partially degraded plant material. The success of the filamentous fungi group in colonizing most natural environments (from Antarctic ice to hot deserts and seawater) can be largely attributed to hyphal growth and branching, allowing an efficient spatial exploration and exploitation of the nutritive resources. Some species, especially pathogens, present a finely tuned regulation between a filamentous growth and a unicellular growth, the latter property being essential for pathogenicity.
Within the Biology group at LIED Paris-Diderot, P. anserina is used as an efficient lab model because:
- it is very easy (and cheap!) to grow,
- the complete sexual cycle can be obtained in vitro in seven days, and yields to the production of sexual spores, named ascospores,
- the availability of its genome sequence has enabled the development of several useful tools in molecular and cellular biology, as well as in cytology.
It hence represents a convenient lab-scale (toy)model for studying the development of filamentous fungi, or even more general living systems networks. The efficient growth of such filamentous fungi is adapted through a mycelial network, in particular in the presence of external constraints disturbing or impeding the environmental exploration. Constraints can be of different nature: e.g. i) chemical/physical like various carbon source, nutrient deficiency/gradient, temperature gradient, hygrometry, electric field, presence of a toxic chemical compound, ii) mechanical like the avoiding of an obstacle or a labyrinthic geometry and also iii) biological like the presence of another organism or the local deletion of the hyphal network.
Note that the biological characterization of P. anserina mutants available at LIED, affected in some key steps of their growth or development, is of interest per se, e.g. for the study of cell wall biogenesis, cellular polarization and branching process.
Developing quantitative tools, in collaboration with physicists, allows to determine the growth velocity of hyphae, to analyze the occurrence of branching and to measure hyphal density over time. Also note that the question of scales is indeed of paramount importance: the hypha is a few microns wide (typically 4 to 6), while the mycelial network can operate on scales ranging from a few square cm up to many square km.
DREAMS : an interdisciplinary project
In this interdisciplinary project, we wish to address the problem of the multi-scale modeling and analysis of expanding dynamical networks under external constraints both by analytical/numerical means and feed-backed lab-scale experimental realizations. The main objectives of our collaboration can be broken down as follows:
- from a biological point of view, we wish to deepen the scientific knowledge of filamentous fungi biology and physiology, which indeed constitutes the main research topic of the B2C group at LIED;
- from a physics point of view, we might wish to try and build the thermodynamic formalism of the metabolism of growth; based on an already on-going collaboration on this topic between LJAD and the Physics group at LIED, we wish to derive from the force-speed relationship of energy conversion machines, such as a muscle, a high-level formalism dedicated to the production of matter and increase in complexity of the thallus;
- from a mathematical point of view, using statistical tools as well as probabilistic and SDE and PDE tools, we wish to build and assess robust and versatile models, analyze their mathematical properties as well as design (and also possibly analyze) adapted efficient numerical methods. We aim at both formal and (possibly) rigorous derivations of the models.
Participants
Yves D'Angelo (Scientific Coordinator), Rémi Catellier, Laurent Monasse, Claire Guerrier , Thierry Goudon (LJAD Nice)
Florence Chapeland-Leclerc, Gwenaël Ruprich-Robert, Eva Cabet (B2C Group, LIED)
Eric Herbert, Cécilia Bobée, Pascal David, Christophe Lalanne, (Physics Group, LIED)
Amandine Véber (MAP5, Paris),
Milica Tomasevic (CMAP, Ecole Polytechnique)
Former participants
Adélaïde Olivier (Math Lab at Orsay),
Franco Flandoli (Scuola Normale di Pisa).
PhD Students and Interns
Clara Ledoux
Moira Lampe
Nicolas Fricker
Sebastian Baudelet
Thibault Chassereau
Lena Kuwata
Aurélien Corrado