| Line 3: | Line 3: | ||
[[File:Flamex.jpg|240px]] | [[File:Flamex.jpg|240px]] | ||
| − | FLAMEX is a suite of solvers able to compute high accuracy solutions to asymptotics-based evolution equations (EE) | + | FLAMEX is a suite of solvers able to compute high accuracy solutions to non-linear non-local asymptotics-based evolution equations (EE), of 1rt |
For propagatong fronts, the EEM (Evolution Equation Modeling) can be found by solving exactly the set of | For propagatong fronts, the EEM (Evolution Equation Modeling) can be found by solving exactly the set of | ||
* Euler equations | * Euler equations | ||
| Line 12: | Line 12: | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |+ Examples of obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts | + | |+ Examples of first-order in time obtained EEM: for 2D planar, 3D planar, or 3D expanding fronts |
|[[File:OUIEEM-1D-2D.png|400 px]] | |[[File:OUIEEM-1D-2D.png|400 px]] | ||
|[[File:OUIEqEEM_1D.png|400 px]] | |[[File:OUIEqEEM_1D.png|400 px]] | ||
| Line 20: | Line 20: | ||
| − | == Main features == | + | == Main features== |
* Solving first-order or second order EE in the Fourier or Fourier-Legendre basis. | * Solving first-order or second order EE in the Fourier or Fourier-Legendre basis. | ||
* Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005) | * Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005) | ||
| + | * EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients.. | ||
* Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence') | * Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence') | ||
| + | == Sample Results == | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Sample results for 3D planar fronts | ||
| + | |[[File:OUIImages_Luk.png|500 px]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | * See some comparisons between FLAMEX and DNS (HALLEGRO) results [http://www.coria-cfd.fr/index.php/H-Allegro#Direct_simulation_of_propagating_flames:_3D_expanding_front_.28Eric_Albin_.26_Yves_D.27Angelo.29] | ||
| + | * More details (and comparisons with experimental results) in [http://dx.doi.org/10.1016/j.ijnonlinmec.2011.05.018], [http://dx.doi.org/10.1016/j.combustflame.2011.12.019] | ||
==Sub-module for asymptotic modeling of Flame-Balls== | ==Sub-module for asymptotic modeling of Flame-Balls== | ||
| − | A sub-module of FLAMEX has also been devoted to the | + | A sub-module of FLAMEX has also been devoted to the solution of flame-balls (FB) dynamics. |
| + | Using a Batchelor approximation for the surrounding Lagrangian flow and | ||
| + | high activation energy asymptotics, we derived a nonlinear forced (stochastic) | ||
| + | integrodifferential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor g(t). | ||
| + | For a diagonal g(t) deduced from random Markov processes of the Ornstein- Uhlenbeck type, | ||
| + | or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that | ||
| + | * flame balls can definitely live for much longer than their time of spontaneous expansion/collapse; | ||
| + | * large enough values of t_life are compatible with Poisson statistics; | ||
| + | * the variations of with the characteristics of g(t) mirror the latter’s statistics, more precisely that of trace(g*g). | ||
| − | == | + | |
| − | + | ||
| − | + | == Participants == | |
| + | Yves D'Angelo, Guy Joulin, Eric Albin, Rui Rego, Gaël Boury, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji. | ||
Revision as of 10:26, 1 April 2016
Contents
The FLAMEX Solver
FLAMEX is a suite of solvers able to compute high accuracy solutions to non-linear non-local asymptotics-based evolution equations (EE), of 1rt For propagatong fronts, the EEM (Evolution Equation Modeling) can be found by solving exactly the set of
- Euler equations
- Rankine-Hugoniot jump relations
- the local kinematic relation defining the local front velocity (e.g. with respect to local curvature).
when the density contrast between 'hot' and 'cold' fluids is asymptotically small.

|
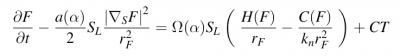
|
Main features
- Solving first-order or second order EE in the Fourier or Fourier-Legendre basis.
- Time resolution using ETDRK1 and 4, using contour integrals to avoid cancelation errors (Trefethen et al. 2005)
- EEM for 2D or 3D planar, 3D expanding/converging fronts, acoustics, fast-transients..
- Laminar or turbulent configurations (EE with additive noise, e.g. Passot-Pouquet, Kraichnan-Celik, Von Karman/Pao or 'DNS turbulence')
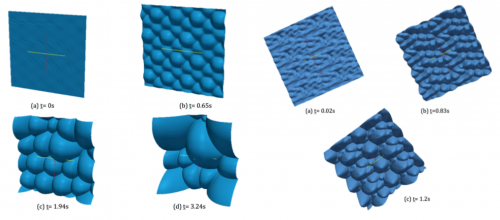
Sample Results
|
- See some comparisons between FLAMEX and DNS (HALLEGRO) results [1]
- More details (and comparisons with experimental results) in [2], [3]
Sub-module for asymptotic modeling of Flame-Balls
A sub-module of FLAMEX has also been devoted to the solution of flame-balls (FB) dynamics. Using a Batchelor approximation for the surrounding Lagrangian flow and high activation energy asymptotics, we derived a nonlinear forced (stochastic)
integrodifferential equation for the current FB radius. This gives access to the FB response to the ambiant Lagrangian rate-of-strain tensor g(t).
For a diagonal g(t) deduced from random Markov processes of the Ornstein- Uhlenbeck type, or linearly filtered versions thereof, extensive numerical simulations and approximate theoretical analyses agree that
- flame balls can definitely live for much longer than their time of spontaneous expansion/collapse;
- large enough values of t_life are compatible with Poisson statistics;
- the variations of with the characteristics of g(t) mirror the latter’s statistics, more precisely that of trace(g*g).
Participants
Yves D'Angelo, Guy Joulin, Eric Albin, Rui Rego, Gaël Boury, Lancelot Boulet, Viphaphorn Srinavawongs, Yosifumi Tsuji.
